TRIGONOMÉTRICA 10
Razones trigonométricas en un triángulo rectángulo
Introducción
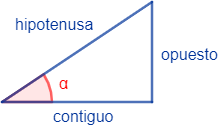
- el cateto opuesto es el que está enfrente del ángulo
- y el cateto contiguo o adyacente es el otro cateto, es decir, el que está en contacto con el ángulo .
- Las razones trigonométricas se definen como la razón entre los lados del triángulo:

Seno

Coseno

Tangente

Cosecante

Secante

Cotangente

EN EL SIGUIENTE LINK PODRÁN ENVIAR PARTE DE LA ACTIVIDAD #1 EN FORMA DE UN CUESTIONARIO, QUE VAN A REALIZAR SEGÚN EL GRADO CORRESPONDIENTE:
Grado 10-6
Grado 10-10
https://forms.gle/cNjscoU9sxLVG9Bc8
Grado 10-13
https://forms.gle/VMgRXT7A5c9GQ4XA6
ACTIVIDADES
ACTIVIDADES
Razones trigonométricas de ángulos notables.
Seno, coseno y tangente de 30º y 60º
 , cada uno de sus tres ángulos mide
, cada uno de sus tres ángulos mide  y, si trazamos una altura del mismo, h, el ángulo del vértice
y, si trazamos una altura del mismo, h, el ángulo del vértice  por el que la hemos trazado queda dividido en dos iguales de
por el que la hemos trazado queda dividido en dos iguales de  cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es:
cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es:




Seno, coseno y tangente de 45º
La diagonal del cuadrado es igual a la hipotenusa de los triángulos formados, aplicamos el teorema de Pitágoras.





Razones trigonométricas de ángulos notables

EN EL SIGUIENTE LINK PODRÁN ENVIAR PARTE DE LA ACTIVIDAD #2 EN FORMA DE UN CUESTIONARIO, QUE VAN A REALIZAR SEGÚN EL GRADO CORRESPONDIENTE:
Grado 10-6
Grado 10-10
https://forms.gle/3tHsi3oAjwAdEAvG7
Grado 10-13
https://forms.gle/X1VR62E2LYrUoqt18
ACTIVIDADES CORRESPONDIENTES AL SEGUNDO PERIODO
https://forms.gle/3tHsi3oAjwAdEAvG7
ÁNGULOS DE ELEVACIÓN Y DEPRESIÓN
El término ángulo de elevación denota al ángulo desde la horizontal hacia arriba a un objeto. Una línea de vista para el observador estaría sobre la horizontal.

EJEMPLOS DE ANGULOS DE ELEVACION
El término ángulo de depresión denota al ángulo desde la horizontal hacia abajo a un objeto. Una línea de vista para el observador estaría debajo de la horizontal.

EJEMPLO DE ANGULO DE DEPRESION
Realiza las siguientes actividades de aprendizaje #1 en tu cuaderno
7)
EN EL SIGUIENTE LINK PODRÁN ENVIAR PARTE DE LA ACTIVIDAD EN FORMA DE UN CUESTIONARIO, QUE VAN A REALIZAR SEGÚN EL GRADO CORRESPONDIENTE:
Teoremas del seno y coseno
Teorema del seno

Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.

AplicacionesEste teorema es útil para resolver problemas si los datos dados entran en alguno de los siguientes casos :
1 Si tenemos las medidas de 2 lados de un triángulo, y el ángulo opuesto a uno de ellos.

Aplicando el teorema inmediatamente puedo obtener el ángulo opuesto al otro lado que conocemos
Ejemplo:
1. Calcula los elementos de un triángulo oblicuángulo si se sabe que: b = 57 cm, c = 35 cm y <B = 42°
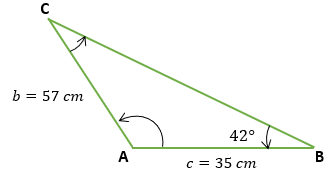
Solución:
Lo primero que tenemos que hacer, es ir recopilando toda la información que nos proporciona el problema del triángulo, que en este caso sería la distancia “c” , la distancia “b” y el ángulo B
c = 35 cm
b = 57 cm
<B = 42°
En la Ley de Senos es importante tener en cuenta nuestra fórmula para aplicarla según sea el caso, en este ejercicio contamos con el lado “b”, así como su ángulo B. Por lo que si tenemos la distancia “c”, entonces será mucho más fácil encontrar el ángulo C
Obteniendo el ángulo C
Aplicando la fórmula de ley de senos, tenemos:

Despejando Sen C, obtenemos:

Sustituyendo datos en la fórmula:

Despeando C

en este caso de despejar "C" en las calculadoras se encuentra con arcsen que es lo mismo que Sen-1 y usualmente se haya presionando la tecla SHIFT y despues la tecla SIN o SEN en la calculadora y aparece Sen-1
Obteniendo el ángulo A
Aplicando la suma interna de los ángulos de un triángulo, tenemos:

Despejando a <A

Simplificando, obtenemos:

Obteniendo el lado a
Para poder encontrar el ultimo elemento de nuestro triángulo, volvemos hacer uso de la ley de senos:

Despejando a la variable “a”

Sustituyendo datos en la fórmula:

Resultados:

2 Si tenemos las medidas de 2 ángulos de un triángulo, y el lado opuesto a uno de ellos.

Aplicando el teorema inmediatamente puedo obtener el lado opuesto al otro ángulo que conocemos.
Ejemplo:
2. En el triángulo ABC, a = 24 cm, <B = 33°, y <A = 108°. Calcula la medida de los lados y ángulos restantes
Solución:
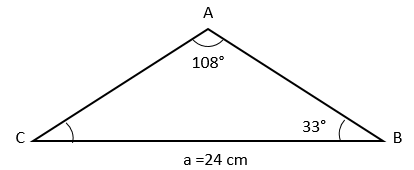
Con los datos obtenidos en el problema, es mucho más fácil hacer la relación de la fórmula a utilizar.
Como deseamos encontrar el lado b y c, podemos aplicar lo siguiente:

Posteriormente, despejar a “b”, quedando así:

Sustituyendo

Podemos ahora calcular el ángulo C, haciendo lo siguiente:

Qué obtendríamos:


Ahora procedemos a calcular el lado “C”
Aplicando la siguiente fórmula:

Obtenemos que:

3 También se puede aplicar cuando se conocen 2 ángulos del triángulo y un lado que no es opuesto a ninguno de ellos, sólo que requiere un paso extra, que es obtener el otro ángulo del triángulo.

Esto es posible porque sabemos que la suma de los ángulos de un triángulo es 180°.
Por ejemplo, en la imagen de arriba, el ángulo B se obtiene de restar los otros 2 ángulos a 180:

Ignorando uno de los ángulos dados originalmente, ya tenemos los datos de 2 ángulos y el lado opuesto de uno de ellos, como el segundo caso mencionado en las aplicaciones.
Ejemplo:
3. Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.

El tercer ángulo del triángulo es:
C = 180° – A – B = 180° – 42° – 75° = 63°
Por la ley de los senos,
Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.

Aplicaciones
Este teorema es útil para resolver problemas si los datos dados entran en alguno de los siguientes casos :
1 Si tenemos las medidas de 2 lados de un triángulo, y el ángulo opuesto a uno de ellos.
Aplicando el teorema inmediatamente puedo obtener el ángulo opuesto al otro lado que conocemos
Ejemplo:
1. Calcula los elementos de un triángulo oblicuángulo si se sabe que: b = 57 cm, c = 35 cm y <B = 42°

Solución:
Lo primero que tenemos que hacer, es ir recopilando toda la información que nos proporciona el problema del triángulo, que en este caso sería la distancia “c” , la distancia “b” y el ángulo B
c = 35 cm
b = 57 cm
<B = 42°
En la Ley de Senos es importante tener en cuenta nuestra fórmula para aplicarla según sea el caso, en este ejercicio contamos con el lado “b”, así como su ángulo B. Por lo que si tenemos la distancia “c”, entonces será mucho más fácil encontrar el ángulo C
Obteniendo el ángulo C
Aplicando la fórmula de ley de senos, tenemos:
Despejando Sen C, obtenemos:
Sustituyendo datos en la fórmula:
Despeando C
en este caso de despejar "C" en las calculadoras se encuentra con arcsen que es lo mismo que Sen-1 y usualmente se haya presionando la tecla SHIFT y despues la tecla SIN o SEN en la calculadora y aparece Sen-1
Obteniendo el ángulo A
Aplicando la suma interna de los ángulos de un triángulo, tenemos:
Despejando a <A
Simplificando, obtenemos:
Obteniendo el lado a
Para poder encontrar el ultimo elemento de nuestro triángulo, volvemos hacer uso de la ley de senos:
Despejando a la variable “a”
Sustituyendo datos en la fórmula:
Resultados:
2 Si tenemos las medidas de 2 ángulos de un triángulo, y el lado opuesto a uno de ellos.
Aplicando el teorema inmediatamente puedo obtener el lado opuesto al otro ángulo que conocemos.
Ejemplo:
2. En el triángulo ABC, a = 24 cm, <B = 33°, y <A = 108°. Calcula la medida de los lados y ángulos restantes
Solución:

Con los datos obtenidos en el problema, es mucho más fácil hacer la relación de la fórmula a utilizar.
Como deseamos encontrar el lado b y c, podemos aplicar lo siguiente:
Posteriormente, despejar a “b”, quedando así:
Sustituyendo
Podemos ahora calcular el ángulo C, haciendo lo siguiente:
Qué obtendríamos:
Ahora procedemos a calcular el lado “C”
Aplicando la siguiente fórmula:
Obtenemos que:
3 También se puede aplicar cuando se conocen 2 ángulos del triángulo y un lado que no es opuesto a ninguno de ellos, sólo que requiere un paso extra, que es obtener el otro ángulo del triángulo.
Esto es posible porque sabemos que la suma de los ángulos de un triángulo es 180°.
Por ejemplo, en la imagen de arriba, el ángulo B se obtiene de restar los otros 2 ángulos a 180:

Ignorando uno de los ángulos dados originalmente, ya tenemos los datos de 2 ángulos y el lado opuesto de uno de ellos, como el segundo caso mencionado en las aplicaciones.
Ejemplo:
3. Dado A = 42°, B = 75° y c = 22 cm. Encuentre el ángulo y los lados faltantes.

El tercer ángulo del triángulo es:
C = 180° – A – B = 180° – 42° – 75° = 63°
Por la ley de los senos,

Por las propiedades de las proporciones


Realiza las siguientes actividades de aprendizaje # 2 teorema del seno en tu cuaderno
1. Dibuja el triangulo y halla los ángulos y los lados que se desconocen. Recordar que los ángulos se escriben con letra mayúscula (A, B, C) y los lados con letra minúscula (a, b, c).
a) Dado ∆ABC con A = 30°, B = 20° y a = 45 mb) Dado ∆ABC con a = 22m, b =12 y A = 40°.c) Dado ∆ABC con A = 80°, B = 70° y a = 100 m d) Dado ∆ABC con A = 35°, B = 65° y a = 98 m

Por las propiedades de las proporciones


2. Resuelve cada triangulo y halla los ángulos y los lados que se desconocen.
a)
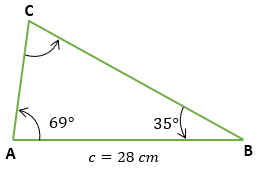
EN EL SIGUIENTE LINK PODRÁN ENVIAR PARTE DE LA ACTIVIDAD LEY DE SENOS EN FORMA DE UN CUESTIONARIO, QUE VAN A REALIZAR SEGÚN EL GRADO CORRESPONDIENTE:
Grado 10-6
Teorema del coseno
 En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

AplicacionesEste teorema es útil para resolver problemas,
1 Si tenemos la medida de un ángulo y de los lados adyacentes a este.

Aplicando el teorema podemos obtener el tercer lado, es decir el lado opuesto al ángulo que tenemos, pues

EJEMPLO:
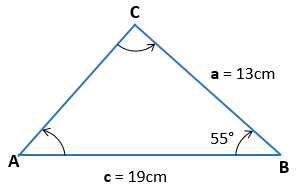
Solución:
Para poder resolver el siguiente ejercicio, asumimos que el lado que deseamos encontrar es el lado b, puesto que el ángulo opuesto es B, entonces nuestra fórmula queda:

De esto resulta


Por lo que:


Ahora tenemos los tres lados de nuestro triángulo, pero nos hace falta conocer los ángulos, para ello, considero un ángulo que deseo calcular que bien puede ser el ángulo A o el ángulo C.
En este caso, elegiré el ángulo A, por lo que mi ecuación quedará:

Sin embargo, el valor del lado a, b y c ya los tengo, entonces procedo a despejar el coseno de A, para resolver.

Despejando aún más…

Invirtiendo la ecuación

Listo, ahora es momento de sustituir nuestros valores:

Ahora aplicando coseno inverso.

Por lo que el ángulo A, es de 42.69 grados.
Ahora mediante la suma de ángulos internos en un triángulo, aplicamos la propiedad para encontrar el ángulo restante:


Despejando a <C

2 Si tenemos la medida de los 3 lados de un triángulo

Aplicando el teorema podemos obtener cualquier ángulo, pues

EJEMPLO:
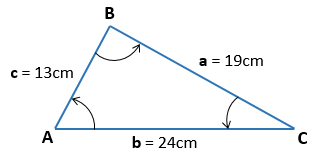
Solución:
Lo primero que tenemos que hacer es recopilar nuestros datos, todo lo que el triángulo oblicuángulo nos ofrece de comienzo, para ello colocamos, los lados:
a = 19 cm.
b = 24 cm.
c = 13 cm.
Vamos a utilizar la fórmula general de la ley de cosenos, siempre y cuando hagamos los despejes correctos para llegar a las nuevas fórmulas que veremos a continuación:



Para cada caso hemos despejado las fórmulas y con ello empezar a sustituir nuestros datos para obtener los valores faltantes de nuestro triángulo.
Para obtener el ángulo A



Despejando A

Listo, ahora veamos como obtener el siguiente ángulo.
Para obtener el ángulo B

Despejando B

Para obtener el ángulo C

Despejando C

Resultados

Comprobación:

FORMULAS DEL TEOREMA DEL COSENO
Realiza las siguientes actividades de aprendizaje #3 teorema del coseno en tu cuaderno
 En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Aplicaciones
Este teorema es útil para resolver problemas,
1 Si tenemos la medida de un ángulo y de los lados adyacentes a este.
Aplicando el teorema podemos obtener el tercer lado, es decir el lado opuesto al ángulo que tenemos, pues


Solución:
Para poder resolver el siguiente ejercicio, asumimos que el lado que deseamos encontrar es el lado b, puesto que el ángulo opuesto es B, entonces nuestra fórmula queda:
De esto resulta
Por lo que:
Ahora tenemos los tres lados de nuestro triángulo, pero nos hace falta conocer los ángulos, para ello, considero un ángulo que deseo calcular que bien puede ser el ángulo A o el ángulo C.
En este caso, elegiré el ángulo A, por lo que mi ecuación quedará:
Sin embargo, el valor del lado a, b y c ya los tengo, entonces procedo a despejar el coseno de A, para resolver.
Despejando aún más…
Invirtiendo la ecuación
Listo, ahora es momento de sustituir nuestros valores:
Ahora aplicando coseno inverso.
Por lo que el ángulo A, es de 42.69 grados.
Ahora mediante la suma de ángulos internos en un triángulo, aplicamos la propiedad para encontrar el ángulo restante:
Despejando a <C
2 Si tenemos la medida de los 3 lados de un triángulo

Aplicando el teorema podemos obtener cualquier ángulo, pues


Solución:
Lo primero que tenemos que hacer es recopilar nuestros datos, todo lo que el triángulo oblicuángulo nos ofrece de comienzo, para ello colocamos, los lados:
a = 19 cm.
b = 24 cm.
c = 13 cm.
Vamos a utilizar la fórmula general de la ley de cosenos, siempre y cuando hagamos los despejes correctos para llegar a las nuevas fórmulas que veremos a continuación:
Para cada caso hemos despejado las fórmulas y con ello empezar a sustituir nuestros datos para obtener los valores faltantes de nuestro triángulo.
Para obtener el ángulo A
Despejando A
Listo, ahora veamos como obtener el siguiente ángulo.
Para obtener el ángulo B
Despejando B
Para obtener el ángulo C
Despejando C
Resultados
Comprobación:
FORMULAS DEL TEOREMA DEL COSENO
Realiza las siguientes actividades de aprendizaje #3 teorema del coseno en tu cuaderno
1. Dibuja el triangulo y halla los ángulos y los lados que se desconocen. Recordar que los ángulos se escriben con letra mayúscula (A, B, C) y los lados con letra minúscula (a, b, c).
a) Dado ∆ABC con b= 70 cm ; c= 85 cm ; a= 100cm
b) Dado ∆ABC con a = 18 m ; B= 65° ; c= 26 cmc) Dado ∆ABC con c= 6 cm ; a= 7.8 cm ; b= 9.5 cmd) Dado ∆ABC con C= 41° ; b= 105 cm ; a= 140 cm
2. Resuelve cada triangulo y halla los ángulos y los lados que se desconocen.
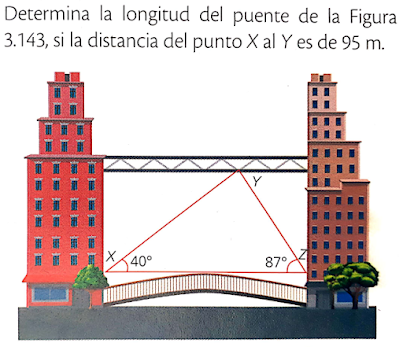
Resolución de problemas
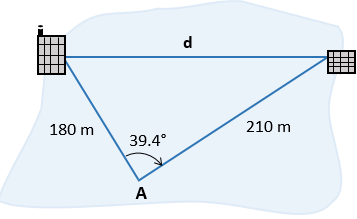
























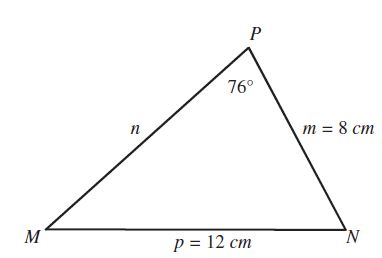








Comentarios
Publicar un comentario